函数的增长

3.1 渐进符号

渐近记号、函数与运行时间

将主要使用渐近记号来描述算法的运行时间。

渐近记号实际上应用于函数

渐近紧确界记号： Θ（big-theta）

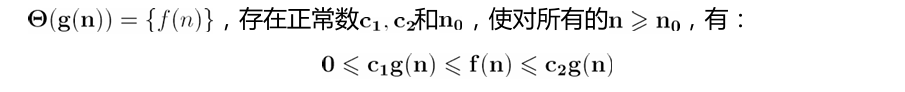
• 通俗理解为f (n) 和g(n)同阶，Θ 用来表示算法的精确阶。

渐近上界记号：O(big-oh)

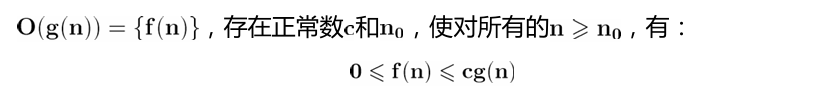
• 通俗的说n满足一定条件范围内，函数f(n)的阶不高于函数g(n)。

[!important]

渐近下界记号：Ω(big-omega)

• 通俗的说n满足一定条件范围内，函数f(n)的阶不低于函数g(n)。

非渐近紧确上界：o(小-oh)

• 通俗理解为f (n) 低于g(n)的阶。
• 例子：f(n) = n^2 + n ,则f(n)=o(n^3)

非渐近紧确下界：ω(小-omega)

• 通俗理解为f (n) 高于g(n)的阶

• ω记号与Ω的关系类似于o和O记号的关系

[!note]

即渐进确界在渐进上界和渐进下界之间

3.2 标准记号与常用函数

向下取整与向上取整

• 其实就是进一或者去尾

模运算