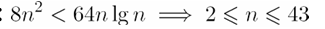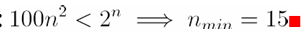1. 算法在计算中的作用
1.1 算法
[!note]
算法是一系列解决问题的明确指令, 也就是说,对于符合一定规范的输入,能够在有限时间内获得要求的输出。
- 算法
- 算法就是任何良定义的计算过程
- 算法是把输入转换成输出的计算步骤的一个序列。
- 算法也可以看成用于求解良说明的计算问题的工具。
- 问题实例由计算该问题解所必需的(满足问题陈述中强加的各种约束的)输入组成。
若对每个输入实例算法都以正确的输出停机,则称该算法是正确的
衡量算法效率的常用标准是速度。
- 算法问题所共有的两个特征:
- 存在许多候选解,但绝大多数候选解都没有解决手头的问题。
- 存在实际应用。
数据结构是一种存储和组织数据的方式
算法的五个特性
- 有穷性:算法必须在有限步骤之后终止
- 确定性:算法的每个步骤都必须精确定义
- 输入(input):有0个或多个输入
- 输出(output):有一个或多个输出
- 可行性:运算都是基本运算,理论上可用纸和笔在有限时间内精确完成
练习
1.1一1 给出现实生活中需要排序的一个例子或者现实生活中需要计算凸壳的一个例子。
- 排序:将一次考试中500名考生的成绩按分数从高到低迕行排名。
- 确定多矩阵相乘的最佳顺序
- 找出凸壳:木板上钉了21个钉子,以其中一些钉子为顶点组成的凸多边形可以包 含所有21个钉子,找出使凸多边形达到最小的所有钉子。
1.1-2 除速度外,在真实环境中还可能使用哪些其他有关效率的量度?
占用资源(内存使用情况,资源利用率)
问题解决程度
答案精度
1.1-3 选择一种你以前巳知的数据结构,并讨论其优势和局限。
- 栈(LIFO)
- 可以严格按照后进先出顺序,非常适合如保存程序调用的返回地址类的特殊应用
- 无法迕行随机读写
- 单链表
- 不需要连续空间,可以以O(1)插入新元素
- 访问为O(n),需要额外空间给指针域使得存储密度小。
1.1-4 前面给出的最短路径与旅行商问题有哪些相似之处?又有哪些不同?
相似:寻求最短路
不同:
- 最短路线问题是找到两点间最短路,不需要经过所有的点
- 旅行商人问题中如果把仓库看做是图中的一个点的话,首先要满足遍历所有的点,然后在所有满足的线路中选择最短的线路,其复 杂程度要高于最短路径。
1.1-5 提供一个现实生活的间题,其中只有最佳解才行。然后提供一个问题,其中近似最佳的 一个解也足够好。
- 看问题需求是求出极端情况(最大化或者最小化)还是可以有误差(近似解)。
1.2 作为一种技术的算法
- 计算时间和存储器空间是一种有限资源,必须被有效的使用,那些时间和空间上有效的算法就有助于做到返一点
像计算机硬件一样把算法看成是一种技术,系统性能不但依赖于选择快速的硬件而且还依赖于选择有效的算法。
练习
2-1 给出在应用层需要算法内容的应用的一个例子,并讨论涉及的算法的功能。
- 计算平均分
- 算法:减少了运算量。最终大大加快了计算效率,幵且提高了计 算准确度。
2-2 假设我们正比较插入排序与归并排序在相同机器上的实现。对规模为n的输入,插入排序运行8*n^2步,而归并排序运行64nlgn步。问对哪些n值,插入排序优于归并排序?
2-3 n 的最小值为何值时,运行时间为 100*n^2 的一个算法在相同机器上快于运行时间为 2^n 的 另一个算法?
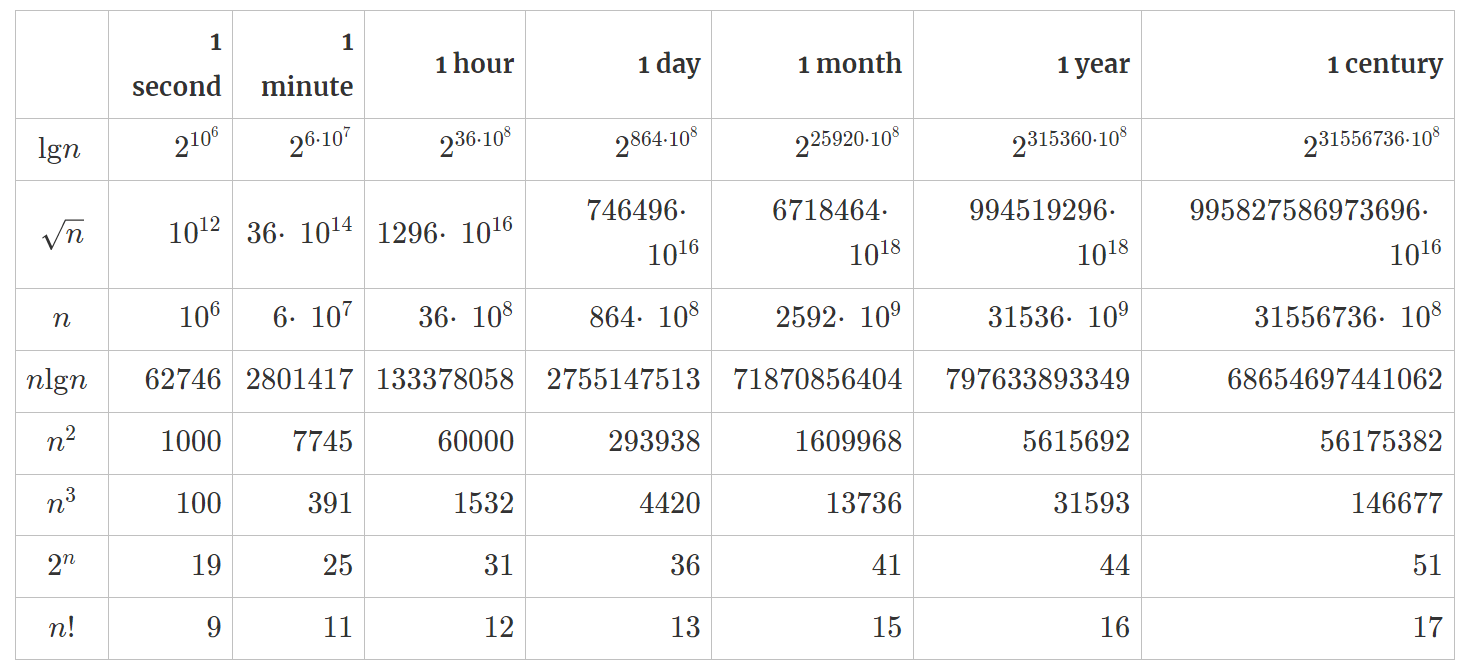
思考题: (运行时间的比较) 假设求解问题的算法需要f(n)毫秒,对下表中的每个函数f(n)和时间 t, 确定可以在时间 t 内求解的问题的最大规模n
评论区 - 01_算法在计算中的作用